梯度下降
-
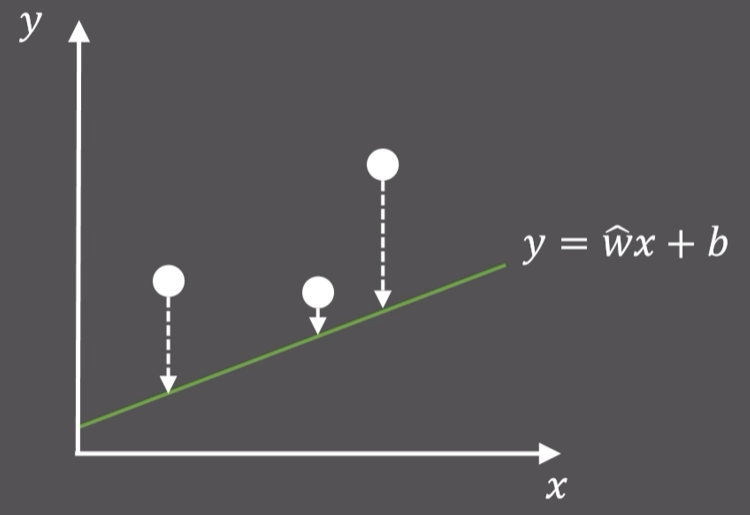
引入: 对下图的三个点进行线性拟合,要优化的参数是$b$,使得三个点到直线的距离最小,我们可以求出距离之和的式子(最小二乘),作为损失函数,在初中我们可以对这个二次函数求最值,现在换个思路,即梯度下降法(GD)
-
随机初始化一个$b$点,求出当前点的斜率,在乘一个常数$\varepsilon$,对$b$进行更新,得到的新值比之前的损失函数更小,然后不断迭代,就找到了最小值
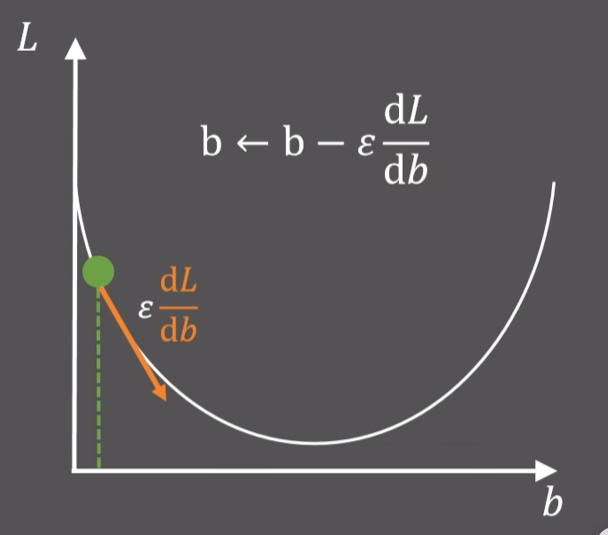
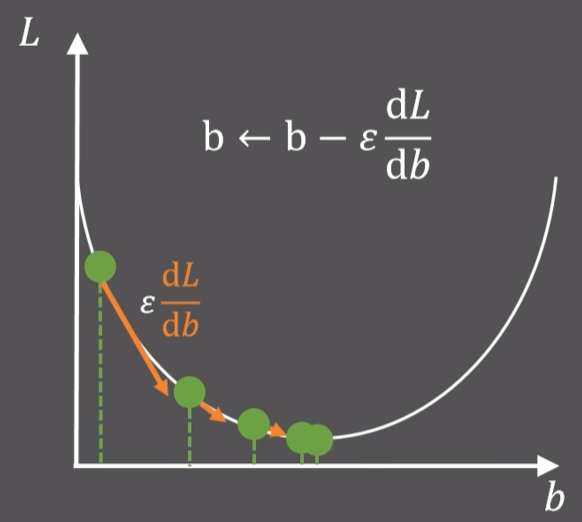
更一般的形式如下:要优化的参数是$\theta$,首先求出$x_i$点处损失函数$L$关于$\theta$的偏导$\nabla_{\theta}L(f(x_i,\theta),y_i)$,对$N$个点求和取平均得到梯度$g$,$\theta$沿着梯度的负方向每次移动一个$\varepsilon$(learning rate)就可以让损失函数更小

-
优化方法:
-
随机梯度下降(SGD):如果样本点很多,计算的内存开销较大,就每次从所有样本中随机选取小部分样本拿来训练,并且不重复
-
动量随机梯度下降:为了防止在 “山谷” 之间 “振荡” ,每次增加一个阻尼,每次计算保留一部分上一次计算的梯度(历史动量),加在一起就是新的梯度
$$
v \leftarrow \alpha v-\varepsilon g \
\theta \leftarrow \theta + v
$$
其中$\alpha$用来控制历史动量对新方向的影响程度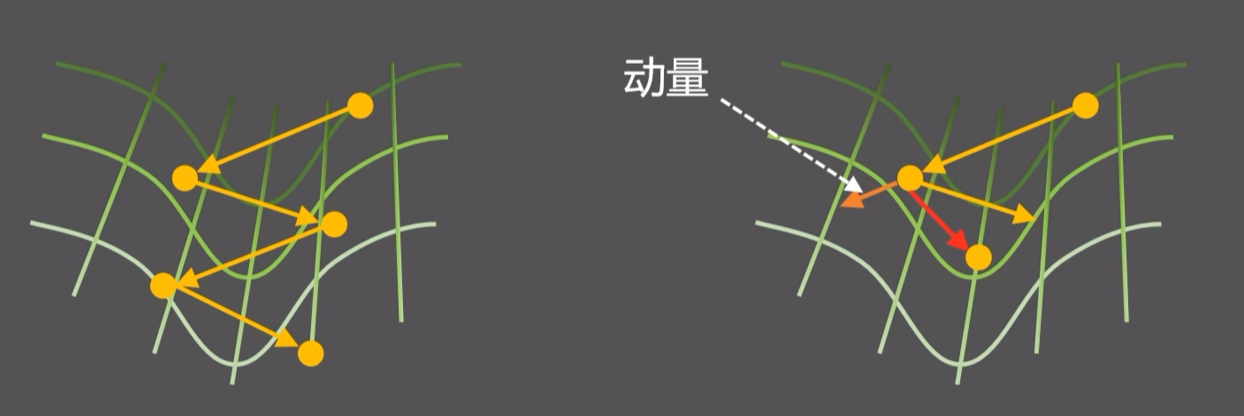
-
AdaGrad算法:在训练过程中希望梯度一开始快速找到下降方向,学习率要大,后期要找到最小值,不能一直震荡,学习率要小。于是引入一个新的量$r$表示梯度在时间上的积累量,然后将$\sqrt{r}$放在学习率的分母上,可以实现自动调整。其中$\delta$是为了稳定数值计算
$$
r \leftarrow r+g^2 \
\theta \leftarrow \theta - \frac{\varepsilon}{\sqrt{r}+\delta}
$$
但AdaGrad算法可能会使学习率过早下降,于是后来提出的RMSProp算法在$r$更新的式子中加入了可以手动调节的$\rho$
$$
r\leftarrow \rho r+(1-\rho)g^2
$$ -
Adam算法:结合自适应学习和动量两种方法,自适应动量由$s$表示
$$
s \leftarrow \rho_1s+(1-\rho_1)g \
r \leftarrow \rho_2r+(1-\rho_2)g^2 \
\hat{s} \leftarrow \frac{s}{1-\rho_1^t} \
\hat{r} \leftarrow \frac{r}{1-\rho_2^t} \
\theta \leftarrow \theta-\frac{\epsilon s}{\sqrt r+\delta}g
$$
-
反向传播
-
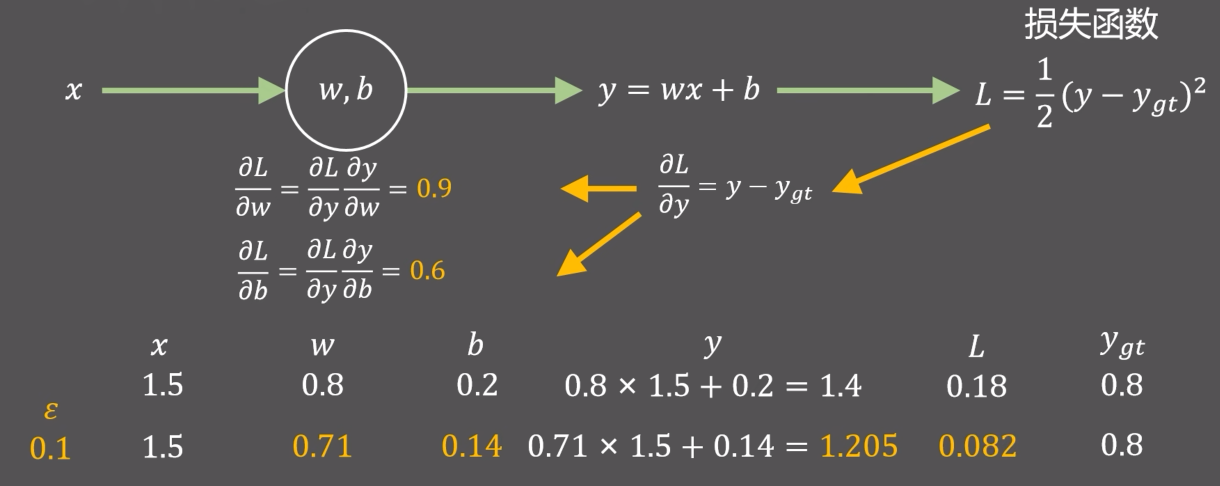
引入:下面是一个线性拟合的例子,$w$和$b$各自随机化一个初始值,通过损失函数去反向更新$w$和$b$的值。根据上面的梯度下降算法,我们需要先计算损失函数$L$对$w$和$b$的梯度值(偏导数),为了方便计算,先计算$L$对$y$的偏导,然后通过链式法则去计算$L$对$w$和$b$的偏导。然后沿着梯度的反方向更新$w$和$b$的值。沿着黄色箭头从后往前计算参数梯度值的方法就是反向传播
反向传播实际就是神经网络中加速计算参数梯度值的方法
-
计算机中的模块化计算(computational graph, 计算图):
下面是正向计算图,输入$x$、$w_1$、$b_1$,输出损失函数$L$的值
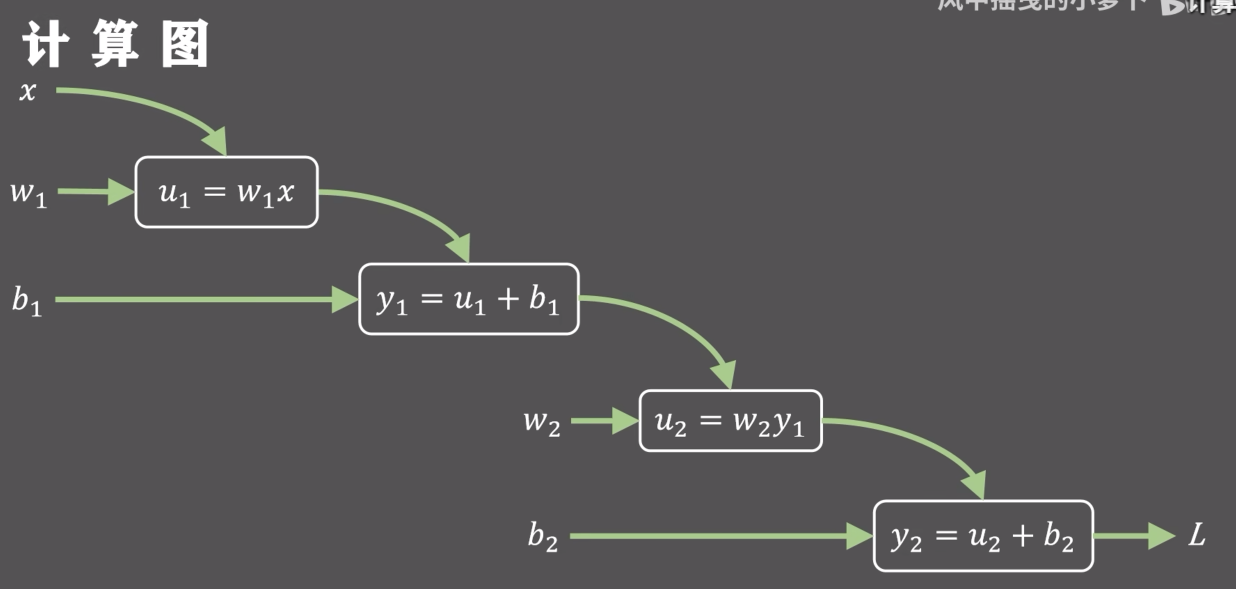
下面是反向传播计算图,
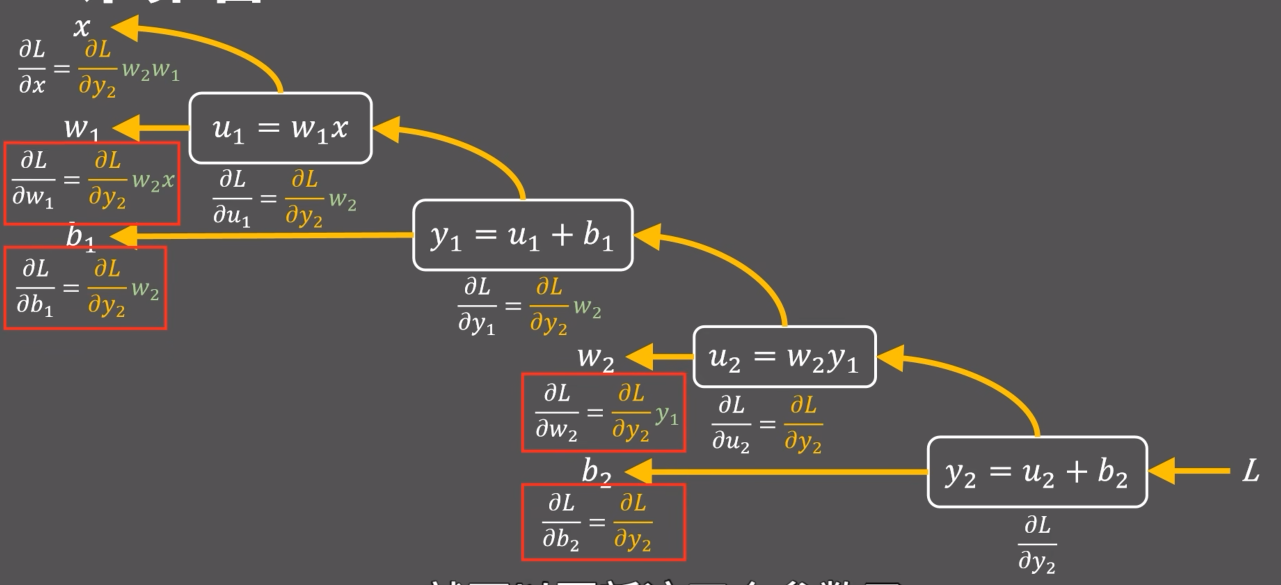
-
代码实现
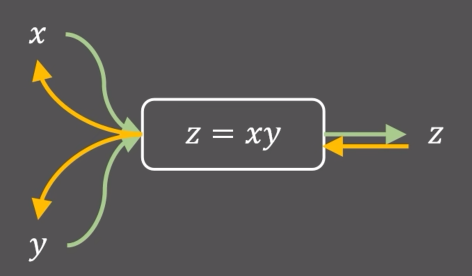
1
2
3
4
5
6
7
8
9
10
11
12
13class Multiply(torch.autograd.Function):
def forward(ctx, x, y):
ctx.save_for_backward(x,y)
z = x * y
return z
def backward(ctx, x, y):
x, y = ctx.save_tensors
grad_x = grad_z * y
grad_y = grad_z * x
return grad_x, grad_y
激活函数
-
神经网络的矩阵乘法只是线性变换,为了解决非线性问题,使用非线性函数进行激活,这就是激活函数
-
激活函数的条件:
- 为了能反向传播,一定要连续可导
- 能映射所有实数
- 激活函数只是增加非线性,不改变对输入的响应状态,应该单调递增
-
常用的激活函数
-
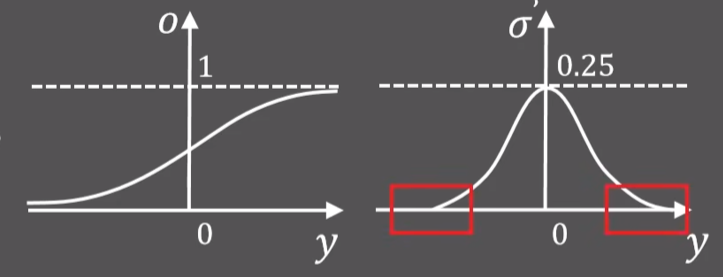
sigmoid函数:$\sigma=\frac{1}{1+e^{-y}}$,导数最大值是0.25,意味着反向更新权重时,每层梯度会至少缩小$1/4$,导致最前面几层梯度几乎为0,权重几乎不更新,这就是梯度消失现象
-
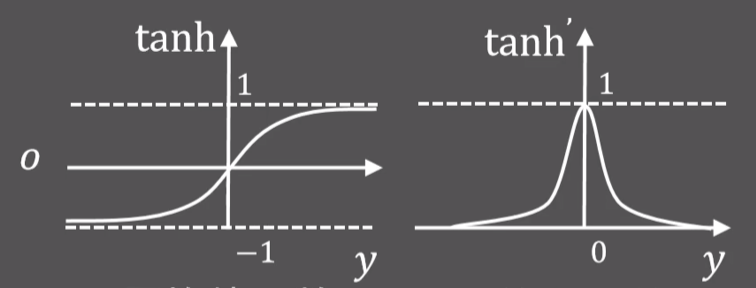
tanh函数:$tanh=\frac{1-e^{-y}}{1+e^{-y}}$,优于sigmoid函数,但也存在梯度消失的问题
-
ReLU函数:$ReLU(y)=\left{
\begin{matrix}
y,y\geq0 \
0,y\leq0
\end{matrix}
\right.$,函数没有上限,梯度累积可能过大导致梯度爆炸具有稀疏性,信息耦合程度低,表现更好
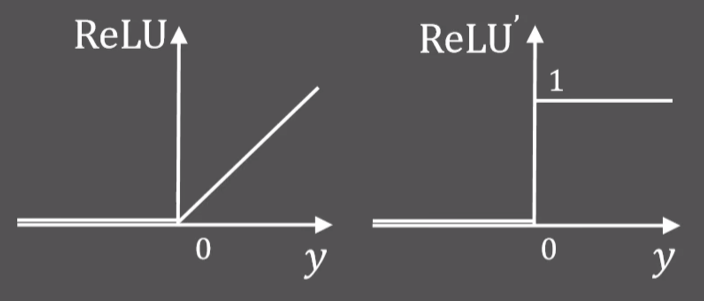
为了避免函数值等于零导致神经元坏死,出现了Leaky ReLU和Parametric ReLU…
-
本着互联网开源的性质,欢迎分享这篇文章,以帮助到更多的人,谢谢!