Leetcode hot 100 writeup
leetcode的判题逻辑 为什么 LeetCode 执行代码正确,提交出错? - 知乎 (zhihu.com)
双指针
移动零
右指针指向下一个零,左指针找到可以交换的值
注意判断条件是l < nums.size() - 1,这是为了防止下标越界
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution {public : void moveZeroes (vector<int >& nums) int l = 0 , r = 0 ; while (r != nums.size () - 1 ) { while (nums[l] != 0 && l < nums.size () - 1 ) l++; r = l; while (nums[r] == 0 && r < nums.size () - 1 ) r++; swap (nums[l], nums[r]); } for (int r = 0 , l = 0 ; r < nums.size (); r++) { while (l < r && nums[l] != 0 ) { l++; } if (nums[r] != 0 ) swap (nums[l], nums[r]); } for (int r = 0 , l = 0 ; r < nums.size (); r++) { if (nums[r] != 0 ) { swap (nums[l], nums[r]); l++; } } } };
我的思路是让左指针依次遍历,右指针去找可以交换的数
根据y总的模板又想了一个思路,右指针正常依次右移,而左指针只有遇到不需要交换的非零数才能右移,直到指向需要交换的零,满足交换条件的交换,y总是真的nb
官方题解的思路是让右指针去依次遍历(此时左右指针指向同一位置),遇到零就不让左指针右移(此时形成快慢指针),下一次循环就可以交换了
盛最多水的容器
这道题是对撞指针,不要想的太复杂,按照直觉每次移动最短的指针即可
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution {public : int maxArea (vector<int >& height) int ans = 0 ; int l = 0 , r = height.size () - 1 ; while (l < r) { ans = max (ans, (r - l) * min (height[l], height[r])); if (height[l] > height[r]) r--; else l++; } return ans; } };
无重复字符的最长子串
这里判断是否出现重复字符是用了一个数组a[],记录了所有ASCII字符出现的次数,大小设为300,可以满足255个ASCII字符的要求
C++中只有全局变量的数组会全部初始化为0,所以这里如果定义局部变量需要手动初始化,为了省事还是以后还是定义成全局变量吧
因为全局变量和静态变量的存储是在程序启动时分配的,存储在程序的静态存储区域中
而局部变量存储在栈上,由于编译器无法确定何时执行初始化操作,就选择了避免额外的开销
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution {public : int lengthOfLongestSubstring (string s) int ans = 0 ; int a[300 ]; for (int i = 0 ; i < 300 ; i++) { a[i] = 0 ; } for (int i = 0 , j = 0 ; i < s.size (); i++) { a[s[i]]++; while (j < i && a[s[i]] > 1 ) { a[s[j]]--; j++; } ans = max (ans, i - j + 1 ); } return ans; } };
普通数组
合并区间
y总的合并区间模板题
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution {public : vector<vector<int >> merge (vector<vector<int >>& intervals) { vector<vector<int >> ans; vector<int > tmp (2 ) ; int st = -2e9 , ed = -2e9 ; sort (intervals.begin (), intervals.end ()); for (auto seg : intervals) { if (seg[0 ] > ed) { tmp[0 ] = st, tmp[1 ] = ed; if (st != -2e9 ) ans.push_back (tmp); st = seg[0 ], ed = seg[1 ]; } else { ed = max (ed, seg[1 ]); } } tmp[0 ] = st, tmp[1 ] = ed; if (st != -2e9 ) ans.push_back (tmp); return ans; } };
轮转数组
最简单的方法直接复制一个数组,注意vector用索引取元素时,初始化要指定vector的长度
复制数组使用assign方法
对于容器类(如vector、list等),assign方法用于将另一个容器的元素赋给当前容器
1 2 3 4 5 6 7 8 9 10 11 class Solution {public : void rotate (vector<int >& nums, int k) int len = nums.size (); vector<int > ans (len) ; for (int i = 0 ; i < len; i++) { ans[(i + k) % len] = nums[i]; } nums.assign (ans.begin (), ans.end ()); } };
官解的第三种方法看起来不是人能想到的
先将所有元素翻转,这样尾部的$k \mod n$个元素就被移至数组头部,然后我们再翻转$[0,(k \mod n)-1]$区间的元素和$[k \mod n,n-1]$区间的元素
原因如下:
1 2 3 4 5 6 7 nums = "----->-->" ; k =3 result = "-->----->" ;reverse "----->-->" we can get "<--<-----" reverse "<--" we can get "--><-----" reverse "<-----" we can get "-->----->" this visualization help me figure it out :)
给出具体代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : void reverse (vector<int >& nums, int start, int end) while (start < end) { swap (nums[start], nums[end]); start++; end--; } } void rotate (vector<int >& nums, int k) int n = nums.size (); reverse (nums, 0 , n - 1 ); reverse (nums, 0 , k % n - 1 ); reverse (nums, k % n, n - 1 ); } };
链表
leetcode中单链表的数据结构
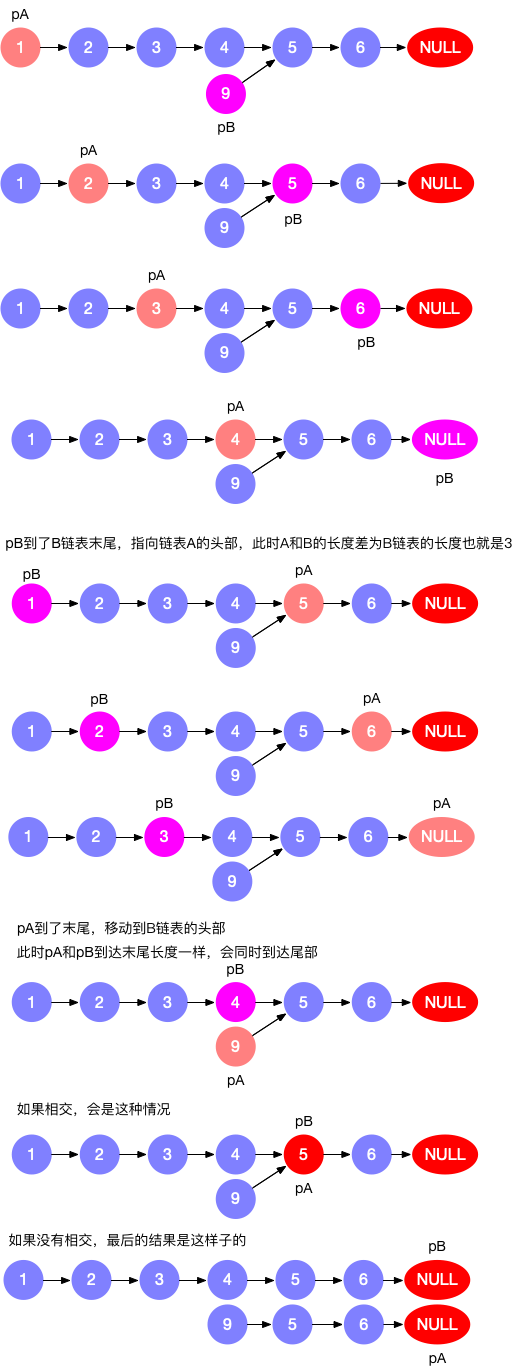
相交链表
这道题如果不考虑空间复杂度,可以先遍历headA,将节点存入一个HashSet,然后遍历headB依次判断是否在哈希表中出现过
官方题解二的时间复杂度是$O(1)$,只能说真的优雅
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution {public : ListNode *getIntersectionNode (ListNode *headA, ListNode *headB) { ListNode *pA = headA, *pB = headB; while (pA != pB) { if (pA) pA = pA->next; else pA = headB; if (pB) pB = pB->next; else pB = headA; } return pA; } };
真的是优雅
看到了一种做法是先求出两个链表的长度,然后遍历长链表至两个链表长度相同,此时同步遍历即可,其实时间复杂度也是$O(2m+2n)=O(m+n)$,我觉得这个比较现实
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution {public : int getLen (ListNode *head) int ans = 0 ; while (head) { ans++; head = head->next; } return ans; } ListNode *getIntersectionNode (ListNode *headA, ListNode *headB) { int lenA = getLen (headA); int lenB = getLen (headB); if (lenA > lenB) { while (lenA != lenB) { headA = headA->next; lenA--; } } else { while (lenA != lenB) { headB = headB->next; lenB--; } } while (headA != headB) { headA = headA->next; headB = headB->next; } if (headA == nullptr ) return nullptr ; else return headA; } };
反转链表
需要设三个指针分别指向prev、curr、next,迭代向后反转,一定要画图理顺思路
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution {public : ListNode* reverseList (ListNode* head) { ListNode* prev = nullptr ; ListNode* curr = head; ListNode* next = nullptr ; while (curr) { next = curr->next; curr->next = prev; prev = curr; curr = next; } return prev; } };
回文链表
其实思路很简单,走到中间,反转后面的链表,然后同步遍历
我下意识就想求出整个链表的长度,但其实没有必要,只是为了走到中间可以使用快慢指针,当快指针走到头时慢指针刚好走到一半的位置
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution {public : ListNode* reverse_list (ListNode* head) { ListNode* prev = nullptr ; ListNode* curr = head; ListNode* next = nullptr ; while (curr) { next = curr->next; curr->next = prev; prev = curr; curr = next; } return prev; } bool isPalindrome (ListNode* head) ListNode* l = head; ListNode* r = head; while (r->next != nullptr && r->next->next != nullptr ) { l = l->next; r = r->next->next; } ListNode* p = reverse_list (l->next); while (p) { if (head->val != p->val) return false ; p = p->next; head = head->next; } return true ; } };
环形链表
快慢指针(双指针)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution {public : bool hasCycle (ListNode *head) if (head == nullptr || head->next == nullptr ) return false ; ListNode* p1 = head; ListNode* p2 = head->next; while (p1 != p2) { if (p2 == nullptr || p2->next == nullptr ) return false ; p1 = p1->next; p2 = p2->next->next; } return true ; } };
合并两个有序链表
类似于归并排序的归并操作,不考虑时间复杂度可以双指针遍历直接新建一个链表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution {public : ListNode* mergeTwoLists (ListNode* list1, ListNode* list2) { ListNode* ans = new ListNode; ListNode* p = ans; while (list1 != nullptr && list2 != nullptr ) { ListNode* tmp = new ListNode; tmp->next = nullptr ; p->next = tmp; p = p->next; if (list1->val < list2->val) { tmp->val = list1->val; list1 = list1->next; } else { tmp->val = list2->val; list2 = list2->next; } } while (list1) { ListNode* tmp = new ListNode; tmp->next = nullptr ; p->next = tmp; p = p->next; tmp->val = list1->val; list1 = list1->next; } while (list2) { ListNode* tmp = new ListNode; tmp->next = nullptr ; p->next = tmp; p = p->next; tmp->val = list2->val; list2 = list2->next; } return ans->next; } };
官方的递归解法非常优雅,时间复杂度为$O(1)$,通过设定一个哨兵节点 prehead来保存起始节点,然后维护一个prev指针,通过改变prev的next来进行合并(可以画图深入理解)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : ListNode* mergeTwoLists (ListNode* list1, ListNode* list2) { ListNode* prehead = new ListNode; ListNode* prev = prehead; while (list1 && list2) { if (list1->val < list2->val) { prev->next = list1; list1 = list1->next; } else { prev->next = list2; list2 = list2->next; } prev = prev->next; } if (list1) prev->next = list1; else prev->next = list2; return prehead->next; } };
环形链表 II
只想到了简单粗暴的哈希表
1 2 3 4 5 6 7 8 9 10 11 12 class Solution {public : ListNode *detectCycle (ListNode *head) { unordered_set<ListNode*> vis; while (head) { if (vis.count (head)) return head; vis.insert (head); head = head->next; } return nullptr ; } };
看了官方题解没想到是一道数学题
首先应该推出快慢指针相遇时慢指针一定还没走完一圈,因为快指针是慢指针速度的两倍,当慢指针走完一圈时,快指针至少走了两圈多,那么快指针一定经过了慢指针一次,那么有没有可能经过但是不相遇呢?不会,因为可以将慢指针看作相对静止,那么快指针每次追一格,只要经过一定相遇
$$
2(a+b)=a+2b+c \\
\Rightarrow a=c
$$
快慢指针相遇时,让一个指针从头节点开始和慢指针一起走,相遇的位置就是环的入口
注意此时的快慢指针应该都从head出发
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : ListNode *detectCycle (ListNode *head) { ListNode *l = head, *r = head; while (r) { if (r->next == nullptr ) return nullptr ; l = l->next; r = r->next->next; if (l == r) { ListNode *p = head; while (p != l) { p = p->next; l = l->next; } return l; } } return nullptr ; } };
两数相加
模拟,注意别忘了cnt记录的进位就行
我通过一个prev指针直接在原链表上修改,空间复杂度应该小于官方题解,但是返回值不计入空间复杂度😢
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution {public : ListNode* addTwoNumbers (ListNode* l1, ListNode* l2) { ListNode *p1 = l1, *p2 = l2, *prev = l1, *prehead = l1; int cnt = 0 , num = 0 ; while (p1 && p2) { num = p1->val + p2->val + cnt; p1->val = num % 10 ; cnt = num / 10 ; prev = p1; p1 = p1->next; p2 = p2->next; } while (p1) { num = p1->val + cnt; p1->val = num % 10 ; cnt = num / 10 ; prev = p1; p1 = p1->next; } if (p2) prev->next = p2; while (p2) { num = p2->val + cnt; p2->val = num % 10 ; cnt = num / 10 ; prev = p2; p2 = p2->next; } if (cnt) { ListNode *p = new ListNode; p->next = nullptr ; p->val = cnt; prev->next = p; } return prehead; } };
删除链表的倒数第 N 个结点
方法一是计算链表长度,第一个指针确定第二个指针要去的位置
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution {public : ListNode* removeNthFromEnd (ListNode* head, int n) { ListNode *prehead = head; ListNode *r = head, *l = head; int num = 0 ; if (!head || !head->next) return nullptr ; while (r) { num++; r = r->next; } if (num == n) { return prehead->next; } for (int i = 0 ; i < num - n - 1 ; i++) { l = l->next; } l->next = l->next->next; return prehead; } };
这道题我做的时候也碰到删除头节点在逻辑上不好处理的情况,我是做了一个特判,官解给出了一个更广泛的方法——哑结点,它的next指针指向链表的头节点,这样就不需要特判,有些复杂的题目特判特别难写
1 2 3 4 5 6 7 8 9 10 11 12 13 int getLength (ListNode* head) ListNode* removeNthFromEnd (ListNode* head, int n) { ListNode* dummy = new ListNode (0 , head); int length = getLength (head); ListNode* cur = dummy; for (int i = 1 ; i < length - n + 1 ; ++i) { cur = cur->next; } cur->next = cur->next->next; ListNode* ans = dummy->next; delete dummy; return ans; }
方法二是快慢指针,r比l超前n个节点,当r遍历到链表的末尾时,l恰好处于倒数第n个节点
方法三是栈,遍历链表的同时将所有节点依次入栈弹出栈的第n个节点就是需要删除的节点
哑巴节点,栈,快慢指针是链表题目的三板斧
两两交换链表中的节点
我的思路是迭代,虽然具体迭代的步骤和官解不太一样(都需要设一个哑节点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : ListNode* swapPairs (ListNode* head) { if (!head) return nullptr ; if (!head->next) return head; ListNode* dummy = new ListNode (0 , head); ListNode *l = dummy, *r = dummy->next, *next = nullptr ; while (r && r->next) { next = r->next->next; r->next->next = l->next; l->next = r->next; r->next = next; l = l->next->next; r = r->next; } return dummy->next; } };
另一种思路是递归
1 2 3 4 5 6 7 8 9 10 class Solution {public : ListNode* swapPairs (ListNode* head) { if (!head || !head->next) return head; ListNode *p = head->next; head->next = swapPairs (head->next->next); p->next = head; return p; } };
二叉树
leetcode中二叉树的数据结构
二叉树的中序遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution {public : vector<int > inOrder; void inOrderTraversal (TreeNode* root) if (root == NULL ) return ; inorderTraversal (root->left); inOrder.push_back (root->val); inorderTraversal (root->right); } vector<int > inorderTraversal (TreeNode* root) { inOrderTraversal (root); return inOrder; } };
二叉树的最大深度
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : void DFS (TreeNode* root, int height, int & max) if (root == nullptr ) return ; height++; if (height > max) { max = height; } DFS (root->left, height, max); DFS (root->right, height, max); } int maxDepth (TreeNode* root) int max = 0 ; DFS (root, 0 , max); return max; } };
翻转二叉树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public : void reverse (TreeNode* root) if (root == nullptr ) return ; TreeNode* node = new TreeNode; node = root->left; root->left = root->right; root->right = node; reverse (root->left); reverse (root->right); } TreeNode* invertTree (TreeNode* root) { reverse (root); return root; } };
对称二叉树
左子树的前序和右子树的后序遍历顺序一样&&即得到结果
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : bool traverse (TreeNode* left, TreeNode* right) if (left == nullptr && right == nullptr ) { return true ; } else if (left == nullptr || right == nullptr ) { return false ; } if (left->val != right->val) { return false ; } return traverse (left->left, right->right) && traverse (left->right, right->left); } bool isSymmetric (TreeNode* root) if (root == nullptr ) return true ; return traverse (root->left, root->right); } };
二叉树的直径(树形DP*)
我的思路是用了一个双递归,相当于第一个递归遍历二叉树的所有节点(每一个都作为转折点遍历一次),第二个递归把该节点的左右子树高度都求出来,注意不需要再-1,因为根节点没有算到路径中,这样一共调用了$n^2$次递归,复杂度太高
但这样相当于对一条路径在每一次节点遍历都计算了一次,其实计算一次就可以了。当前节点的直径等于左右子树的最长链相加。于是求直径实际上就是求深度,只不过是在求深度的同时可以计算出直径。通过一个全局变量ans可以记录最大直径 求直径 => 求深度
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution {public : int MAX = 0 ; void DFS (TreeNode* root, int temp, int & max) if (root == nullptr ) { return ; } temp++; if (temp > max) { max = temp; } DFS (root->left, temp, max); DFS (root->right, temp, max); } int diameterOfBinaryTree (TreeNode* root) if (root == nullptr ) { return 0 ; } int max = 0 , maxl = 0 , maxr = 0 ; int temp = 0 ; DFS (root->left, temp, maxl); DFS (root->right, temp, maxr); max = maxl + maxr; if (max > MAX) { MAX = max; } diameterOfBinaryTree (root->left); diameterOfBinaryTree (root->right); return MAX; } };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : int ans = 0 ; int dfs (TreeNode* root) if (root == nullptr ) { return 0 ; } int L = dfs (root->left); int R = dfs (root->right); ans = max (ans, L + R + 1 ); return max (L + 1 , R + 1 ); } int diameterOfBinaryTree (TreeNode* root) dfs (root); return ans - 1 ; } };
二叉树的层序遍历
循环的开始阶段队列中的元素就是位于同一层的所有元素
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution {public : vector<vector<int >> levelOrder (TreeNode* root) { queue<TreeNode*> q; vector<vector<int >> ans; if (root == nullptr ) { return ans; } q.push (root); while (!q.empty ()) { vector<int > vc; int size = q.size (); for (int i = 0 ; i < size; i++) { TreeNode* p = q.front (); q.pop (); vc.push_back (p->val); if (p->left != nullptr ) { q.push (p->left); } if (p->right != nullptr ) { q.push (p->right); } } ans.push_back (vc); } return ans; } };
将有序数组转换为二叉搜索树
第一反应AVL板子题,但是一想这也太麻烦了,其实就是根据中序遍历序列确定AVL,由于平衡的要求,每次递归都以中间的节点作为根节点,有点像根据中序和前/后序构造二叉树
为什么可以不用板子呢?因为题目并不是根据输入序列依次去插入节点构造(答案唯一),而是这些节点只要能构造出一棵AVL就行(答案不唯一)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : TreeNode* build_tree (vector<int >& nums, int left, int right) { if (left > right) return nullptr ; int mid = (left + right) / 2 ; TreeNode* p = new TreeNode; p->val = nums[mid]; p->left = build_tree (nums, left, mid - 1 ); p->right = build_tree (nums, mid + 1 , right); return p; } TreeNode* sortedArrayToBST (vector<int >& nums) { return build_tree (nums, 0 , nums.size () - 1 ); } };
验证二叉搜索树
一开始读错题了,这棵BST是有条件的:节点的左(右)子树只包含小于(大于)当前节点的数。所以需要知道左右子树上的极值
最开始我希望通过引用传递来维护一个左子树的最大值和右子树的最小值,从下往上判断,但是如果同时传入min和max的话最大值(最小值)会被右子树(左子树)更新,这是不允许的。所以只把一个边界传进去,这样其实就不需要传递引用了,还是自上而下判断,每次传入左(右)子树不能大于(小于)的值,实际就是当前节点的值,一旦不满足递增(减)的规律就返回false
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public : typedef long long ll; bool dfs (TreeNode* root, ll max, ll min) if (root == nullptr ) { return true ; } ll value = (ll)root->val; if (dfs (root->left, max, value) && dfs (root->right, value, min) && value > max && value < min) { return true ; } return false ; } bool isValidBST (TreeNode* root) return dfs (root, LONG_MIN, LONG_MAX); } };
下面是官方的wp,helper函数用于判断子树的范围是否在$(\text{lower},\text{upper})$的范围内。和我的代码只是抽象出来的逻辑不太一样,但代码逻辑是一样的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution {public : bool helper (TreeNode* root, long long lower, long long upper) if (root == nullptr ) { return true ; } if (root -> val <= lower || root -> val >= upper) { return false ; } return helper (root -> left, lower, root -> val) && helper (root -> right, root -> val, upper); } bool isValidBST (TreeNode* root) return helper (root, LONG_MIN, LONG_MAX); } };
BST题目很重要的一条性质是中序遍历是递增序列,这道题也可以使用这一性质
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution {public : bool isValidBST (TreeNode* root) stack<TreeNode*> stack; long long inorder = (long long )INT_MIN - 1 ; while (!stack.empty () || root != nullptr ) { while (root != nullptr ) { stack.push (root); root = root -> left; } root = stack.top (); stack.pop (); if (root -> val <= inorder) { return false ; } inorder = root -> val; root = root -> right; } return true ; } };
二叉搜索树中第K小的元素
第一种方法是朴实无华的中序遍历,用stack(迭代)模拟递归,这样不用完成整个遍历和存储结果
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : vector<TreeNode*> v; void inOrder (TreeNode* root) if (root == nullptr ) { return ; } inOrder (root->left); v.push_back (root); inOrder (root->right); } int kthSmallest (TreeNode* root, int k) inOrder (root); return v[k-1 ]->val; } };
如果你需要频繁地查找第k小的值,你将如何优化算法?
第二种方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 ``` ### 二叉树的右视图 其实就是层序遍历,把每一层遍历的最后一个树加到`ans`中即可 ```c++ class Solution {public : vector<int > rightSideView (TreeNode* root) { vector<int > ans; queue<TreeNode*> q; TreeNode* p = root; if (root != nullptr ) { q.push (p); } while (!q.empty ()) { int num = q.size (); for (int i = 0 ; i < num; i++) { p = q.front (); if (p->left != nullptr ) { q.push (p->left); } if (p->right != nullptr ) { q.push (p->right); } q.pop (); } ans.push_back (p->val); } return ans; } };
二叉树展开为链表
这道题的价值在于:使用原地算法(O(1)额外空间)展开这棵树
从前序与中序遍历序列构造二叉树
PAT做过,很老的题了
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution {public : TreeNode* build (int root, int left, int right, vector<int >& preorder, vector<int >& inorder) if (left > right) { return nullptr ; } TreeNode* p = new TreeNode (); int idx = -1 ; for (int i = left; i <= right; i++) { if (inorder[i] == preorder[root]) { idx = i; break ; } } if (idx == -1 ) { return nullptr ; } p->val = preorder[root]; p->left = build (root + 1 , left, idx - 1 , preorder, inorder); p->right = build (root + (idx - left) + 1 , idx + 1 , right, preorder, inorder); return p; } TreeNode* buildTree (vector<int >& preorder, vector<int >& inorder) { return build (0 , 0 , inorder.size () - 1 , preorder, inorder); } };
回溯
全排列
N 皇后
很经典的DFS例题,y总DFS讲的例题就是这个。col、dg、udg三个数组用来剪枝
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution {public : vector<vector<string>> ans; bool col[10 ] = {false }; bool dg[20 ] = {false }; bool udg[20 ] = {false }; int num = 0 ; void dfs (vector<string> temp, int row) if (row == num) { ans.push_back (temp); return ; } for (int i = 0 ; i < num; i++) { if (col[i] == false && dg[i+row] == false && udg[num+i-row] == false ) { col[i] = true ; dg[i+row] = true ; udg[num+i-row] = true ; string s = string (i, '.' ) + "Q" + string (num - 1 - i, '.' ); temp.push_back (s); dfs (temp, row + 1 ); temp.pop_back (); col[i] = false ; dg[i+row] = false ; udg[num+i-row] = false ; } } } vector<vector<string>> solveNQueens (int n) { vector<string> temp; num = n; dfs (temp, 0 ); return ans; } };
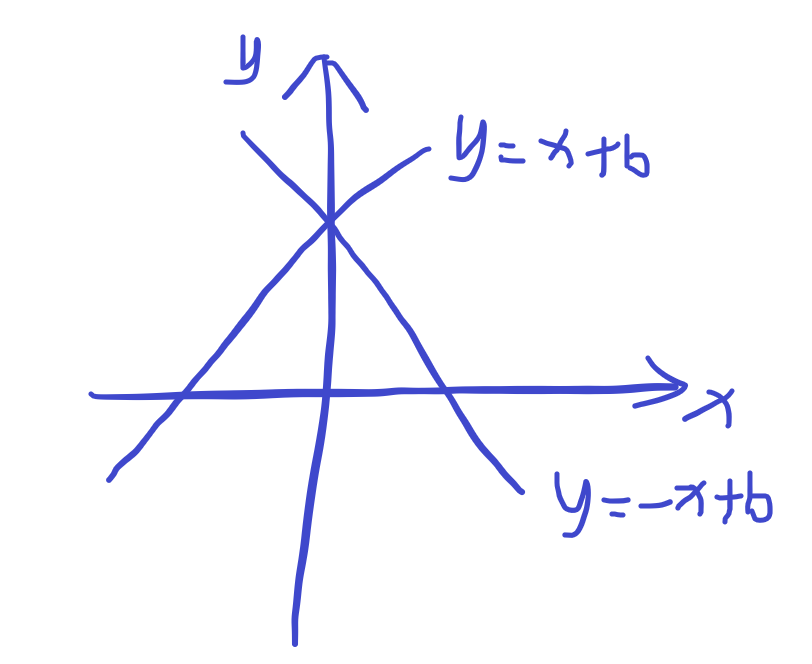
如何确定某一元素在对角线dg和反对角线udg的位置
截距$b$有$y+x$和$y-x$两种情况,为了防止出现负数加个$n$,即$y+x$和$y-x+n$
还有更加原始的一种搜索方式,遍历$n^2$个格子,每个格子只有放和不放两种选择,这说明即使同一个题目,抽象出来的程度不一样,搜索的方式也不一样
二分
搜索插入位置
分界条件是大于等于目标值,取后面一段的左边界,注意插入到序列最后面的特殊情况
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : int searchInsert (vector<int >& nums, int target) int l = 0 , r = nums.size () - 1 ; while (l < r) { int mid = l + r >> 1 ; if (nums[mid] >= target) { r = mid; } else { l = mid + 1 ; } } if (l == nums.size () - 1 && nums[l] < target) { return l + 1 ; } return l; } };
搜索二维矩阵
相除和取余分别求出横纵坐标即可
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public : bool searchMatrix (vector<vector<int >>& matrix, int target) int s1 = matrix.size (), s2 = matrix[0 ].size (); int l = 0 , r = s1 * s2 - 1 ; while (l < r) { int mid = l + r + 1 >> 1 ; if (matrix[mid / s2][mid % s2] <= target) { l = mid; } else { r = mid - 1 ; } } if (matrix[l / s2][l % s2] == target) return true ; else return false ; } };
在排序数组中查找元素的第一个和最后一个位置
需要求两个边界点,第一个是大于等于目标值段的左边界点,第二个是小于等于目标值段的右边界点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution {public : vector<int > searchRange (vector<int >& nums, int target) { vector<int > ans; if (nums.size () == 0 ) return vector<int > {-1 , -1 }; int l = 0 , r = nums.size () - 1 ; while (l < r) { int mid = (l + r) >> 1 ; if (nums[mid] >= target) { r = mid; } else { l = mid + 1 ; } } if (nums[l] != target) return vector<int > {-1 , -1 }; else ans.push_back (l); l = 0 ; r = nums.size () - 1 ; while (l < r) { int mid = (l + r + 1 ) >> 1 ; if (nums[mid] <= target) { l = mid; } else { r = mid - 1 ; } } ans.push_back (l); return ans; } };
搜索旋转排序数组
在笔记中我写了这样一句话:
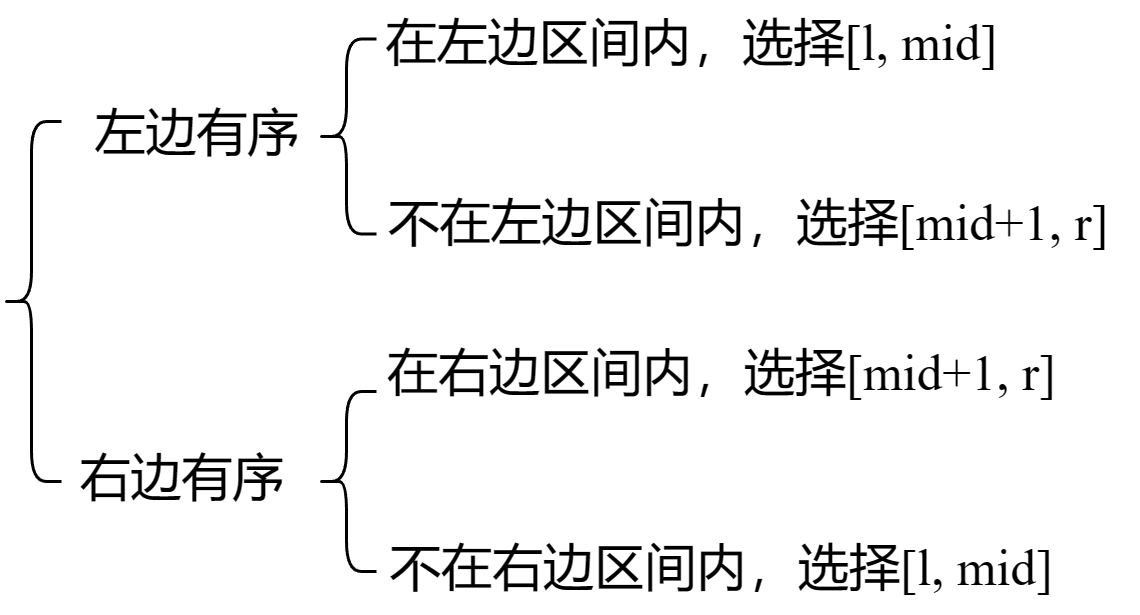
整数二分的核心思路是每次选择答案所在的区间,这可以将答案的范围缩小一半
这题的关键就是如何选择下一次的答案区间。以mid = l + r >> 1作为分界点,可以将整个区间分成[l, mid]和[mid + 1, r],虽然由于旋转,mid两端不再都是有序序列,但是一定是一端有序一端无序,于是我们可以根据有序部分判断出target在哪一端
这道题的难点在于边界条件的确定,一定要将区间明确地分成两份
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution {public : int search (vector<int >& nums, int target) int l = 0 , r = nums.size () - 1 ; while (l < r) { int mid = l + r >> 1 ; if (nums[l] <= nums[mid]) { if (target >= nums[l] && target <= nums[mid]) { r = mid; } else { l = mid + 1 ; } } else { if (target >= nums[mid + 1 ] && target <= nums[r]) { l = mid + 1 ; } else { r = mid; } } } if (nums[l] == target) return l; else return -1 ; } };
寻找旋转排序数组中的最小值
栈
有效的括号
这道题官解使用了一个map来映射括号对非常巧妙,可以避免写一堆if语句,并且具有很好的扩展性
一开始我将栈定义成char类型的结果部分样例出现了下标越界的报错,还没搞懂是为什么
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution {public : unordered_map<char , char > pairs = { {')' , '(' }, {']' , '[' }, {'}' , '{' } }; bool isValid (string s) int n = s.size (); if (n % 2 == 1 ) { return false ; } int stk[n+1 ], tt = 0 ; for (int i = 0 ; i < n; i++) { char ch = s[i]; if (pairs.count (ch)) { if (stk[tt] == pairs[ch]) { tt--; } else { return false ; } } else { stk[++tt] = ch; } } return tt == 0 ; } };
每日温度
单调栈的应用,为了方便求出下标差,栈中存储的应该是下标而不是元素的值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution {public : int stk[1000100 ], tt; vector<int > dailyTemperatures (vector<int >& nums) { vector<int > ans (nums.size()) ; for (int i = nums.size () - 1 ; i >= 0 ; i--) { while (tt && nums[stk[tt]] <= nums[i]) tt--; if (tt) ans[i] = stk[tt] - i; else ans[i] = 0 ; stk[++tt] = i; } return ans; } };
本着互联网开源的性质,欢迎分享这篇文章,以帮助到更多的人,谢谢!
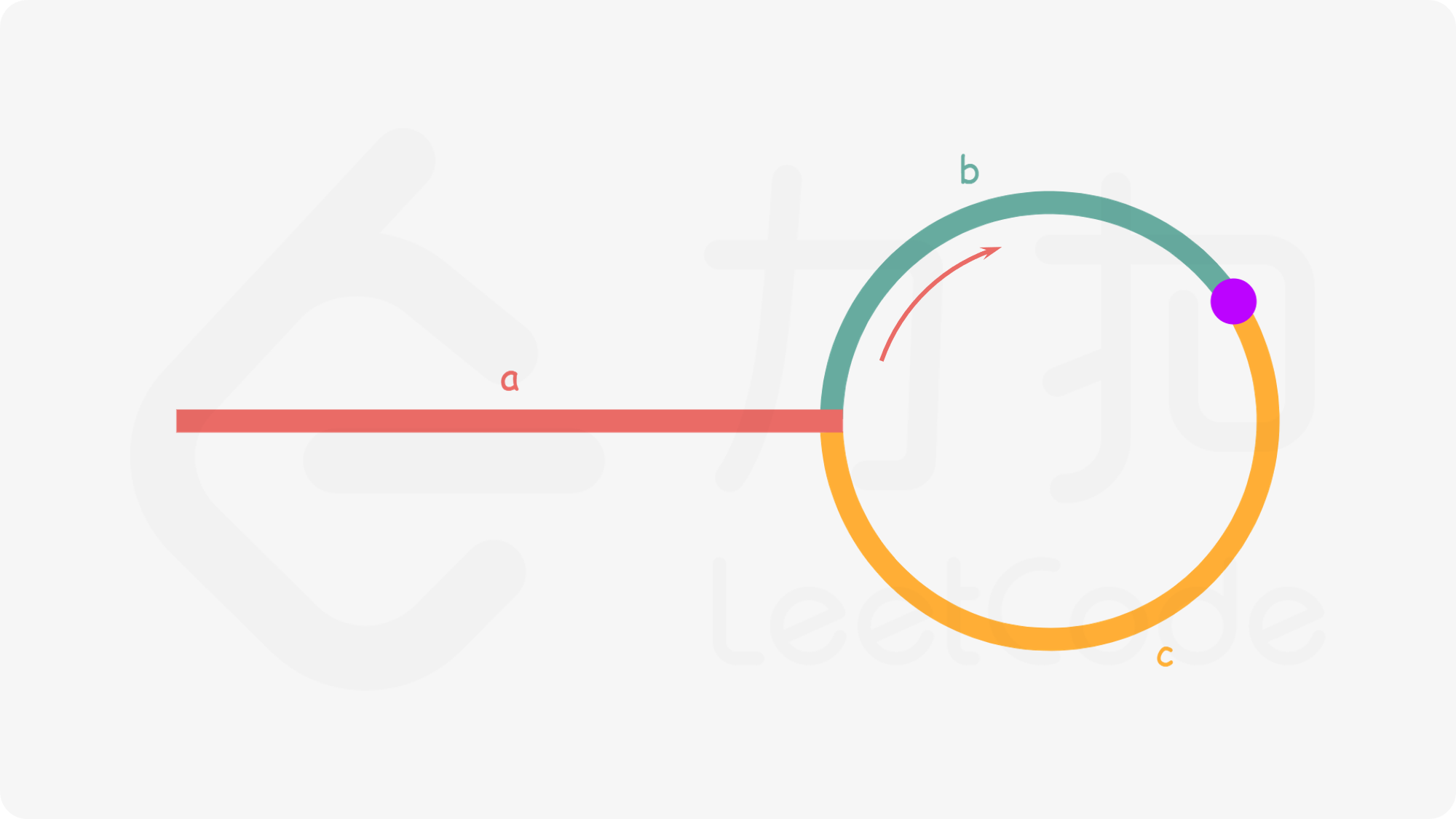 $$
2(a+b)=a+2b+c \\
\Rightarrow a=c
$$
快慢指针相遇时,让一个指针从头节点开始和慢指针一起走,相遇的位置就是环的入口
$$
2(a+b)=a+2b+c \\
\Rightarrow a=c
$$
快慢指针相遇时,让一个指针从头节点开始和慢指针一起走,相遇的位置就是环的入口